Почему геометрию часто называют "холодной" и "сухой"? Одна из причин заключается в ее неспособности описать форму облака, горы, береговой линии или дерева. Облака - не сферы, горы - не конусы, береговые линии - не окружности, древесная кора не гладкая, молния распространяется не по прямой. В более общем плане я утверждаю, что многие объекты в Природе настолько иррегулярные и фрагментированы, что по сравнению с Евклидом Природа обладает не просто большей сложностью, а сложностью совершенно иного уровня. Число различных масштабов длины природных объектов для всех практических целей бесконечно.
Существует большое число математических объектов называемых фракталами: треугольник Серпинского, снежинка Коха, кривая Пеано, множество Мандельброта, лоренцевы аттракторы. Фракталы с большой точностью описывают многие физические явления и природные образования: горы, облака, турбулентные течения, корни, ветви и листья деревьев, кровеносные сосуды, что далеко не соответствует простым геометрическим фигурам. Впервые фрактальную природу нашего мира подметил математик Бенуа Мандельброт.Согласно Мандельброту, слово фрактал происходит от латинских слов fractus - дробный и frangere - ломать, что отражает суть фрактала, как "изломанного", нерегулярного множества. Мандельброт дал строгое математическое определение фрактала, однако он так и не был удовлетворен этим определением, так как оно не включает в себя некоторые множества, рассматриваемые многими математиками, как фракталы. Тем не менее, для того, чтобы создать для себя некое представление о фракталах, достаточно понять следующее несложное, но и не строгое, определение: фрактал – это множество, которое состоит из частей, в некотором смысле "подобных" ему самому.
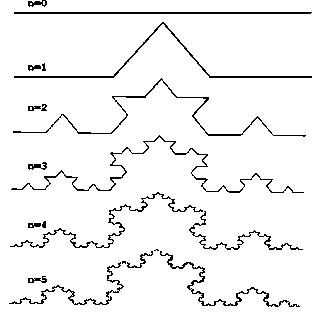
В качестве примера рассмотрим один из таких фрактальных объектов - триадную кривую Кох. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Далее каждый из отрезков полученной кривой, заменяется точно так же. Полученная кривая кроме самоподобия обладает ещё одним интересным свойством: очевидно, что предел длины кривой при n, стремящемся к бесконечности, где n – количество таких операций, равен бесконечности. В итоге получили кривую бесконечной длины, заполняющую ограниченное множество на плоскости, что само по себе очень любопытно.

Одним из очень красивых фрактальных является множество Мандельброта, которое относится к классу алгебраических фракталов. При создании этого множества (и вообще любого алгебраического фрактала) есть некий процесс, в котором каждый следующий элемент зависит от предыдущего (в данном случае Zn+1=Zn2+C, где Z и C – комплексные числа, а Z0=0). Этот процесс, в зависимости от начальных условий (C), может быть устойчив, то есть не "уходить" от "нулевых" условий ("нулевыми" условиями могут являться и начальные), больше чем на какое-то M (|Zn| <M), а может быть неустойчив. Поскольку всегда есть вероятность того, что процесс, однажды "ушедший далеко", "вернётся" в устойчивое состояние или что процесс, долго находящийся в устойчивом состоянии, внезапно станет неустойчивым, то точно проверить, устойчив ли процесс при данных начальных условиях, нельзя. Поэтому мерой устойчивости процесса являются то, как быстро процесс "уйдёт" дальше чем на M. Поскольку можно провести лишь конечное число операций, то выбирается некое I – количество итераций, после которого считается, что процесс абсолютно устойчив.
Для получения графического изображения используется многоцветное изображение. Пусть у нас имеется N цветов (от 0 до N-1). Цвет точки с координатами (x,y) считается так: C присваивается комплексное значение x+i*y, далее проводится итерации, пока либо процесс не "уйдёт" дальше чем на M, либо не будут выполнены все I итераций. Если k – количество итераций, которое было выполнено, то цвет точки выбирается по формуле [(N-1)*k/I], где квадратные скобки обозначают целую часть.
Описанный алгоритм реализует и написанные мной программы. Обе программы изображает множество начальных условий от (-2,-1.25) до (1.3333333 33,1.25) (макроопределения PMIN, QMIN, PMAX, QMAX), максимальное количество итераций равно (макроопределение MaxIteration) 256, M (макроопределение BigNumber) равняется 10, при подсчёте используется тип (макроопределение FTYPE) float. Также в программах есть возможность увеличивать изображение. После прорисовки изображения, можно нажать на клавишу "*", в этом случае будет перерисовано начальное изображение. Если нажать на клавишу "-", то будет показано изображение, нарисованное до последнего увеличения. Если же нажать на любую другую клавишу, то в центре экрана появится мерцающая точка, которую можно двигать стрелками на один пиксель, при включённом NumLock на дополнительной клавиатуре пиксель можно двигать на 10 пикселей. После нажатия на пробел таким же образом выбирается вторая точка, которая появляется на месте первой. После второго нажатия на пробел полученный прямоугольник увеличивается на весь экран.
Разница между программами в том, что одна из (рис. 2) них использует стандартную графическую библиотеку и поэтому она использует разрешение 640x480 при 16 цветах.
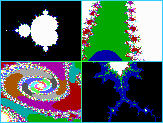
Вторая же (Рис. 3) использует графическую библиотеку TGE (The Graphics Engine version 1.41), зарегистрированная версия которой была любезно предоставлена её автором Маттеем Хилдебран (Matthew Hildebrand) в качестве благодарности за найденные мной ошибки в незарегистрированной версии этой же программы. Эта библиотека поддерживает графические режимы вплоть до 1280x1024 при 256 цветах. Моя же программа использует лишь разрешение 1024x768 при 256 цветах.

1. Untitled.Da.Ru / Полет мысли / Фракталы / Дополнение http://untitled.agava.ru/thinks/fractal/addon.shtml.
2. ВВЕДЕНИЕ ВО ФРАКТАЛЫ http://home.ural.ru/~shabun/fractals/fractals.htm.
3. Говорим по-русски 09.11.1999 23:21 - 11.11.1999 06:26 http://saturn.spaceports.com/~speakrus/f014.htm (письмо с темой "Дмитрию Самойлову о фракталах").
4. Красота фракталов http://www.iph.ras.ru:8101/~mifs/rus/danilov.htm.
5. О фракталах http://www.chat.ru/~fractals/math.htm.
6. Фракталы, синтез изображений http://www.visti.net/cplusp/all_96/6n96y/6n96y1a.htm.